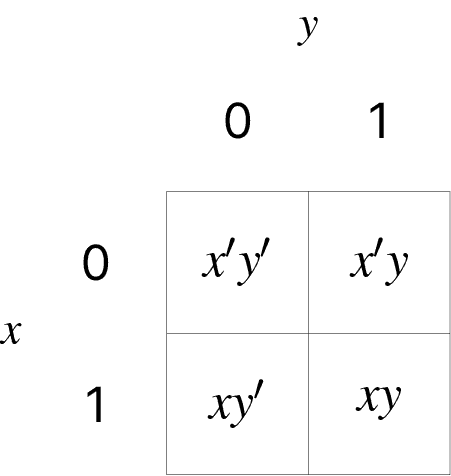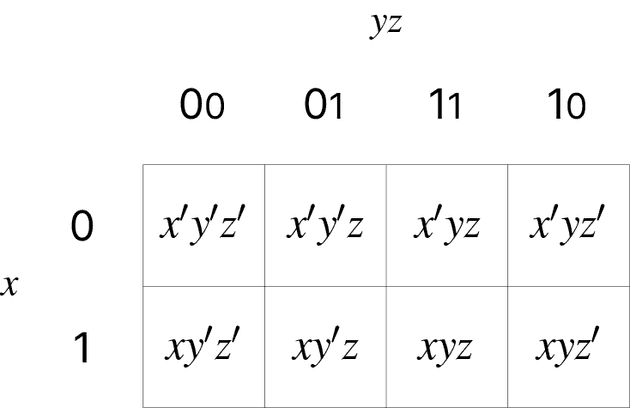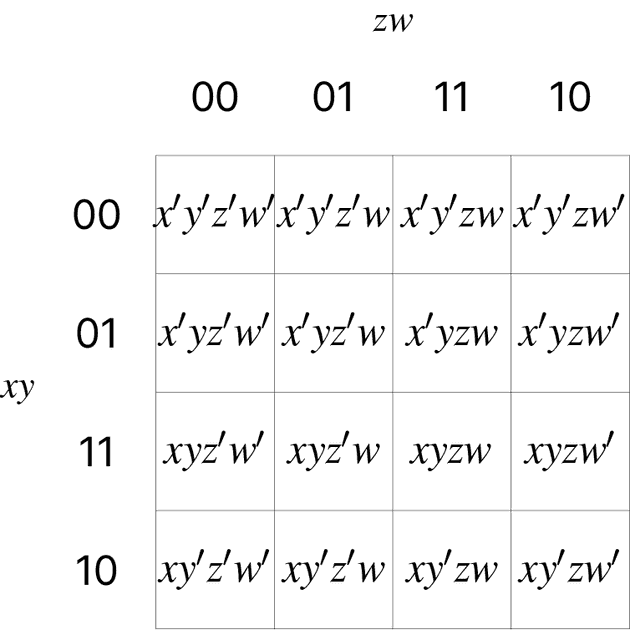본 포스트의 내용은 2022년 2학기 이산수학 과목을 수강하며 공부한 내용 중 기말고사 시험 범위에 해당하는 내용을 정리한 문서로, 로 작성된 파일을 pandoc을 이용하여 Markdown으로 변환한 문서입니다.
제가 모르는 부분 또는 생소한 부분 위주로 정리한 노트이므로, 생략된 부분이 있어 본 포스트만 참고할 경우 이해에 어려움이 있을 수 있으니, 참고 바랍니다.
원본 파일의 내용을 확인하고 싶으시다면, 여기를 클릭하여 원본 .tex파일이나, 여기를 눌러 .pdf 파일을 확인하실 수 있습니다.
Week 9
관계
-
서로 다른 두 집합에 속하는 원소들 간의 순서Order를 표현
-
순서쌍 집합(곱집합의 부분 집합)에 속하면서 순서쌍을 이루는 원소들은 '관계'가 있다
이항 관계Binary Relation
집합 에서 집합 로 가는 관계
: 의 부분 집합
일 때, ;
정의역Domain:
공변역Codomain:
치역Range:
항 관계-ray Relation:
의 부분 집합
역관계Inverse Relations: 에서 로의 관계,
, 존재
존재
관계의 표현
서술식 방법
e.g.) 에서 원소 가 인 관계
나열식 방법
-
화살표 도표Arrow diagram
-
좌표 도표Coordinate diagram
- 집합 의 원소를 축 위의 점으로, 의 원소를 축 위의 점으로 표시
-
방향 그래프Directed graph
-
관계 이 하나의 집합 에 대한 관계 표현일 때
-
의 각 원소 그래프의 정점Vertex
-
이면 에서 로 화살표가 있는 연결선Edge로 표현
-
-
관계 행렬Relation matrix
-
부울Boolean 행렬 이용
-
에서 로 가는 관계 에 대한 행렬
-
e.g.) 과 의 이항 관계
-
관계의 성질
-
반사 관계Reflexive Relation
- 모든 에 대해 인 관계,
-
비반사 관계Irreflexive Relation
- 모든 에 대해 인 관계,
-
반사 관계도 비반사 관계도 아닌 경우
-
대칭 관계Symmetric Relation
-
에 대해 이면 , 존재 존재
-
관계 행렬에서 대각 성분 기준으로 대칭이면 대칭 관계 성립
-
-
반대칭 관계
-
에 대해 이고, 이면
-
이고, 이면
-
-
추이 관계
- 에 대해 이고, 이면 인 관계
합성 관계Composite Relation
에서 로의 관계 과, 에서 로의 관계 에 대해서, 에서 로의 합성 관계 또는
- 합성 관계의 연산:
e.g.)
-
합성 관계의 거듭제곱
-
기타 연산
-
추이 관계와 합성 관계
[정리] 추이 관계와 거듭제곱의 관계:
집합 에 대한 관계 이 추이 관계일 필요충분조건은 모든 양의 정수 에 대하여 이다.
폐포Closure
폐포Closure: 상의 관계 이 어떤 성질을 만족하지 않을 때, 그
성질을 만족하도록 순서쌍들을 추가하여 (원하는 성질이 만족되는 가장
작은 집합)로 확장
성질 에 대한 관계 의 폐포: 에 대한 관계 에 대해, 가
을 포함하면서 성질 를 가질 때, 는 에 대한 의 폐포
반사 폐포Reflexive Closure
에 대해, 을 포함하면서 반사 관계를 갖는 관계
대칭 폐포Symmetric Closure
에 대해, 을 포함하면서 대칭 관계를 갖는 관계
추이 폐포Transitive Closure
에 대해, 을 포함하면서 추이 관계를 갖는 관계
연결 관계Connectivity Relation
연결 관계 는 의 추이 폐포
[정리] 이 개의 원소를 갖는 집합에 대한 관계이고, 을 관계 에 대한 부울 행렬이라고 했을 때, 의 추이 폐포 는
예제 풀이
양의 정수Positive Integer 집합에서 두 원소 에 대해서 '가 를 나눈다'라는 관계는 어떤 성질을 만족하는가? (관계(1) 강의 참조)
Week 10
동치 관계Equivalence Relation
반사 관계, 대칭 관계, 추이 관계가 모두 성립하는 경우
동치류Equivalence Class
에 대한 관계 이 동치 관계일 때, 에 대한 의 동치류: 와
순서쌍을 이루는 원소들의 집합
동치 관계와 분할Partitions
-
분할: 공집합이 아닌 집합 의 분할 조건 (는 의 부분 집합)
-
-
동치류와 분할: 에 대한 관계 이 동치 관계일 때, 동치류 집합 는 다음 만족함
-
일 때,
-
-
면,
-
부분 순서 관계
- 순서 관계: 집합 원소들 간 순서를 나타내기 위한 순서 관계
e.g.)
프로젝트에서 수행해야 할 작업들의 집합에서 작업 에 대해 가 보다 먼저 수행되어야 한다면 의 순서쌍으로 구성되는 순서 관계
수학의 대소 관계인 의 순서 관계, 가 보다 작다
-
부분 순서 관계Partially Ordered Relation: 집합 에 대한 관계 이 반사, 반대칭, 추이 관계일 때 관계
-
부분 순서 집합Partially Order Set, Poset: 이 에 대한 부분 순서 관계이면 순서쌍
-
부분Partial이라는 용어를 쓰는 이유: 집합 의 원소의 모든 쌍이 관계를 가지는 것은 아니기 때문
-
부분 순서 집합 기호: 은 의 부분 순서 관계
-
집합 에 대한 관계 이 부분 순서 관계
-
의 두 원소 에 대하여 을 로 표기
-
'가 를 선행한다' ( precedes )라고 읽음
-
-
비교 가능Comparable: 부분 순서 집합 에서 가 또는 이면 와 는 비교 가능
e.g.) 자연수들의 집합 상의 관계 '배수이다'라고 할 때, 자연수 3과 9는 비교 가능한가? 또, 7과 4는 비교 가능한가?
-
이므로 3과 9는 비교 가능하다.
-
이므로 4와 7은 비교 가능하지 않다.
-
선형 순서Linear Order
-
이 부분 순서를 만족
-
만약 라면 또는 중 하나가 성립
-
-
선형 순서 집합Linearly Ordered Set: 집합 의 모든 두 원소가 비교 가능하면 는 선형 순서 집합
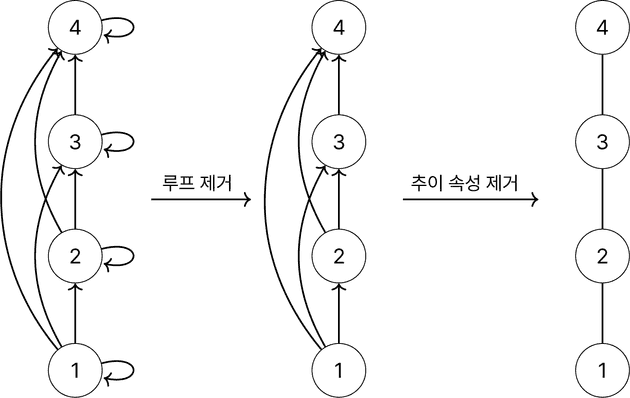
하세 도표Hasse Diagram
-
부분 순서 집합 을 그림으로 표현
-
독일의 수학자 하세가 고안
-
방향 그래프의 일종으로서 화살표는 표시하지 않고 모든 연결선Edge을 트리Tree와 같이 모두 아래 방향을 향하도록 그림
-
부분 순서 관계에 대한 방향 그래프에서 루프는 생략
-
부분 순서 집합 의 원소 에 대해 고, 면, 정점 를 정점 보다 아래쪽에 그림
-
고 일 때, 고 면서 인 가 집합 에 존재하지 않으면 에서 로 가는 선을 그림
집합 의 멱집합Power Set 에 대한 부분 집합 관계의 부분 순서 집합 에 대한 하세 도표를 그려라
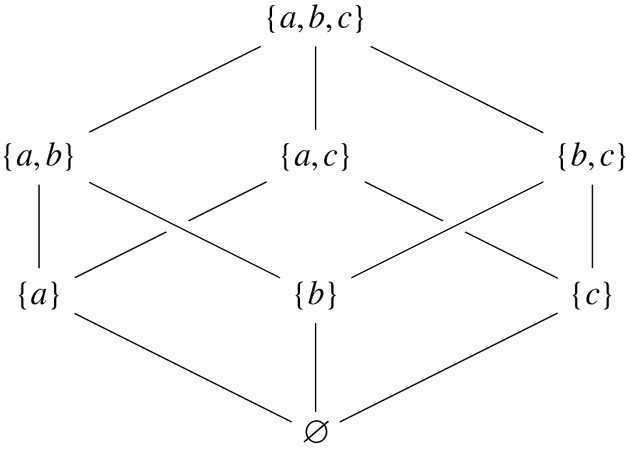
극대 원소와 극소 원소
부분 순서 집합 가 있을 때
-
극대 원소Maximal Element: 의 원소 에 대하여 인 원소 가 에 존재하지 않을 때 원소 , 위의 하세 도표에서 에 해당
-
극소 원소Minimal Element: 인 원소 가 에 존재하지 않을 때 원소 , 위의 하세 도표에서 에 해당
최대 원소와 최소 원소
- 최대 원소Greatest Element: 어떤 가 의 모든 원소 에 대해 이면, 를 의 최대 원소
- 최소 원소Least Element: 어떤 가 의 모든 원소 에 대해 이면, 를 의 최소 원소
함수Function
집합 에 대해 집합 에서 로 가는 관계가 성립할 때, 에 대해 하나가 대응되는 관계
-
대응Correspondence: 집합 가 있을 때, 에 가 확정되는 경우 '는 에 대응'
-
에서
-
정의역Domain:
-
공변역Codomain:
-
상Image: 함수값,
-
치역Range: 상의 집합,
-
함수 vs 관계
-
관계
-
B의 원소와 대응하지 않는 A의 원소 존재 가능
-
하나의 A의 원소가 하나 이상의 B의 원소와 대응 가능
-
-
함수
-
A의 모든 원소는 B의 원소와 무조건 대응
-
하나의 A의 원소가 하나의 B의 원소와 대응
-
하나의 B의 원소가 하나 이상의 A의 원소와 대응 가능
-
단사 함수Injective Function
-
정의역 의 모든 원소들이 공변역 의 서로 다른 원소와 대응
-
일대일 함수One-to-one Function
-
에 대하여 이면 성립
-
단사 함수에서 함수의 치역은 공변역의 부분 집합
-
에서
-
단조 증가 함수Strictly Increasing Function:
-
단조 감소 함수Strictly Decresaing Function:
- c.f.) 단조 증가 함수와 단조 감소 함수는 단사 함수
-
특성: 의 모든 원소가 의 원소와 반드시 대응하는 것은 아니므로, 성립
전사 함수Surjective Function
-
공변역 의 모든 원소가 정의역예 대응
-
치역 = 공변역,
-
모든 함수의 관계가 의 모든 원소에 반영되므로 반영 함수Onto Function
특성: 의 모든 원소가 의 원소와 대응되어야 하므로 성립
전단사 함수Bijective Function
-
집합 의 모든 원소들이 집합 의 모든 원소와 하나씩 대응
-
일대일 대응 함수One-to-one Correspondence Function
특성: 의 모든 원소가 의 모든 원소와 하나씩 일대일 대응되므로
합성 함수Composition Function
결합 법칙 성립:
교환 법칙 성립 X
-
특징
-
에 대해 가 합성함수일 때
-
와 가 단사 함수면, 도 단사 함수다
-
와 가 전사 함수면, 도 전사 함수다
-
와 가 전단사 함수면, 도 전단사 함수다
-
가 단사 함수면, 도 단사함수다
-
가 전사 함수면, 도 단사함수다
-
가 전단사 함수면, 는 단사함수고 는 단사함수다
-
항등 함수Identity Function
전단사 함수라고도 함
함수 고, 집합 에 대한 항등 함수가 , 집합 에 대한
항등 함수가 일 때,
역함수Inverse Function
전단사 함수일 때만 역함수 존재
항등 함수와 역함수
전단사 함수 에 대해, 다음이 성립
상수 함수Constant Function
특성 함수Characteristic Function
올림 함수Ceiling Function, 내림 함수Floor Function
올림 함수, 천정 함수 / 최소 정수 함수Least Integer Function:
내림 함수, 바닥 함수 / 최대 정수 함수Greatest Integer Function:
Week 11
그래프Graph
공집합이 아닌 정점Vertex or Node의 집합 와 서로 다른 정점의 쌍 를 연결하는 변 또는 연결선Edge의 집합 로 구성되는 구조
\
무방향 그래프Undirected Graph: 특별한 언급 없으면 무방향 그래프
방향 그래프Directed Graph, Digraph: 선행자 후속자
단순 그래프Simple Graph: 루프가 없는 그래프
멀티 그래프Multigraph:
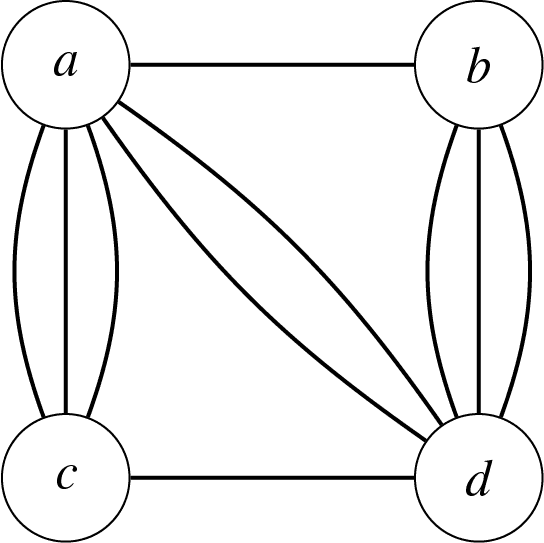
연결 그래프Connected Graph: 모든 Vertex가 연결된 그래프, 모든
Vertex간 경로 존재
강한 연결 그래프Strongly Connected Graph: 방향 그래프에서만, 모든 두
Vertex 에 대해
연결 요소Connectivity Component: 그래프에서 모든 Vertex들이 연결되어
있는 부분 그래프
연결 수Connectivity Number: 에서 연결 요소 개수
그래프 용어
인접Adjacent과 근접Incident:
루프Loop:
-
경로Path: Vertex들의 열Sequence 에서 , 경로의 길이는
-
단순 경로Simple Path: 같은 Edge를 두 번 포함하지 않는 경로
-
기본 경로Elementary Path: 같은 Node를 두 번 포함하지 않는 경로
-
-
사이클Cycle 또는 순회Circuit: 인 경로, 종점 == 시점
-
단순 사이클Simple Cycle: 같은 Edge를 반복해 방문하지 않는 사이클
-
기본 사이클Elementary Cycle: 시점 제외 어떤 Node도 반복해 방문하지 않는 사이클
-
-
길이Length: 경로 또는 사이클을 구성하는 Edge의 수
-
차수Degree : Vertex 에 근접하는 Edge의 수, Loop는 두 개로 Count
-
홀수점Odd Vertex: 차수가 홀수인 Vertex
-
짝수점Even Vertex: 차수가 짝수인 Vertex
-
-
외차수Out-degree : 방향 그래프에서 Vertex 에서 시작하는 화살표 수
-
내차수In-degree : 방향 그래프에서 Vertex 에서 끝나는 화살표 수
[정리] 차수에 대한 정리
- 에서, 모든 Vertex의 차수의 합은 Edge의 수의 두 배
- 에서, 차수가 홀수인 정점의 수는 짝수
오일러 경로Eulerian Path 및 오일러 회로Eulerian Circuit
- 오일러 경로: 멀티 그래프에서 모든 Edge들을 한 번씩만 통과하는 경로를 찾는 문제
- 오일러 회로: Node는 여러 번 통과할 수 있지만, Edge는 한 번씩만 통과하는 사이클
- 어떤 그래프 가 오일러 경로를 가지기 위한 필요충분조건은 가 연결 그래프이고, 홀수 차수의 개수가 또는 인 경우이다.
- 어떤 그래프 가 오일러 회로를 가지기 위한 필요충분조건은 가 연결 그래프이고, 모든 Node들이 짝수 개의 차수를 가지는 경우이다.
해밀턴 경로Hamiltonian Path 및 해밀턴 회로Hamiltonian Circuit
-
해밀턴 경로: 그래프에서 모든 Node를 오직 한 번씩만 지나지만 시점으로 돌아오지 않는 경로
-
해밀턴 회로: 그래프에서 모든 Node를 오직 한 번씩만 지나는 순회
-
해밀턴 회로에 대한 충분 조건:
-
차수 1을 갖는 Node를 가진 그래프는 해밀턴 순환을 가질 수 없다.
-
차수가 2인 Node에 근접하는 두 Vertex는 해밀턴 순환에 포함된다.
-
한 Node에 근접하는 두 Vertex가 해밀턴 순환에 포함되면, 그 Node에 근접한 다른 Vertex는 해밀턴 순환에 포함될 수 없다.
-
Ore's Theorem: 일 때, 개의 Node를 갖는 단순 연결 그래프
에서 인접하지 않은 임의의 정점 에 대해 이면
는 해밀턴 그래프이다.
Dirac's Theorem: 일 때, 개의 Node를 갖는 단순 연결 그래프
에서 임의의 정점 에 대해 이면 는 해밀턴
그래프이다.
특수 형태의 그래프
- 가중 그래프Weight Graph
- 의 각 Edge에 보다 큰 수가 할당되었을 때, 이 값을 가중값Weight이라고 하며, 이를 가중 그래프라고 한다.
- 동형 그래프Isomorphic Graph
- 과 가 주어졌을 때, 전단사 함수 가 존재하여 이면 를 동형Isomorphism이라고 하고, 과 를 동형 그래프라 한다.

오일러의 정리
연결된 평면 그래프 에서 Vertex의 수를 , Edge의 수를 , 면Space의 수를 라고 할 때,
평면 그래프
평면 그래프Planar Graph: 를 평면에 그릴 때, 교차하지 않는
그래프
면 의 차수 : 평면 그래프의 면 의 경계를 이루는 변의 수
e.g.)
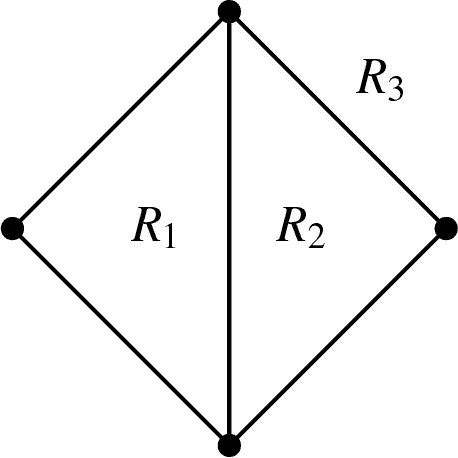
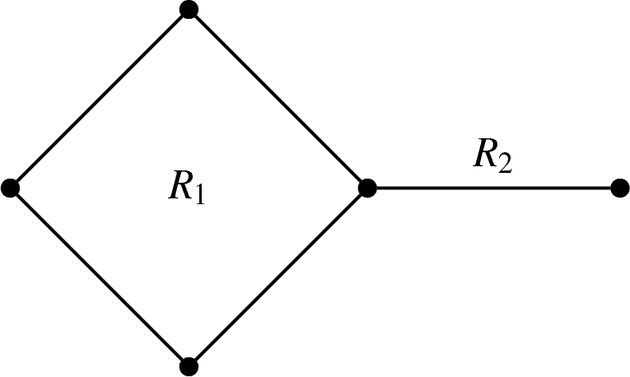
평면 그래프의 면의 차수의 총 합은 변의 수의 두 배이다.
연결된 평면 단순 그래프의 Vertex의 수를 , Edge의 수를 라 할 때,
이면
모든 면의 차수는 3이상이므로,
Week 12
특수 형태의 그래프
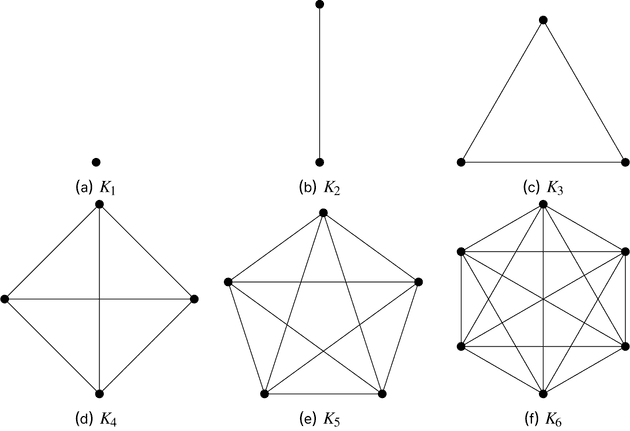
- 완전 그래프Complete Graph
- 모든 개의 Vertex들의 쌍 사이에 Edge가 존재하는
- 이분 그래프Bipartite Graph
- 가 와 로 나누어져, 각 Edge가 X 내의 Vertex와 Y 내의 Vertex의 쌍으로 연결될 때,
- 완전 이분 그래프Complete Bipartite Graph
- 내의 모든 Vertex와 내의 모든 Vertex 사이에 Edge가 존재할 때, 그래프
그래프의 표현 방법
- 인접 행렬Adjacency Matrix
- 에서, 일 때, 의 인접 행렬은 행렬
-
인접 리스트Adjacency List
- 각 Vertex에 대해 포인터가 주어지고, 그 Vertex로 부터 인접한 Vertex들을 모두 Linked List에 담음 (List 내에서는 순서에 관계가 없음)
-
Linked List는 Node의 연결로 표현
-
Head: Linked List의 시작 Node (그래프의 각 Vertex들)
-
Node: 데이터 필드 + 포인트 필드 (다음에 연결된 Node의 주소 저장)
-
마지막 Node의 포인트 필드는
null
-
그래프의 응용 및 활용
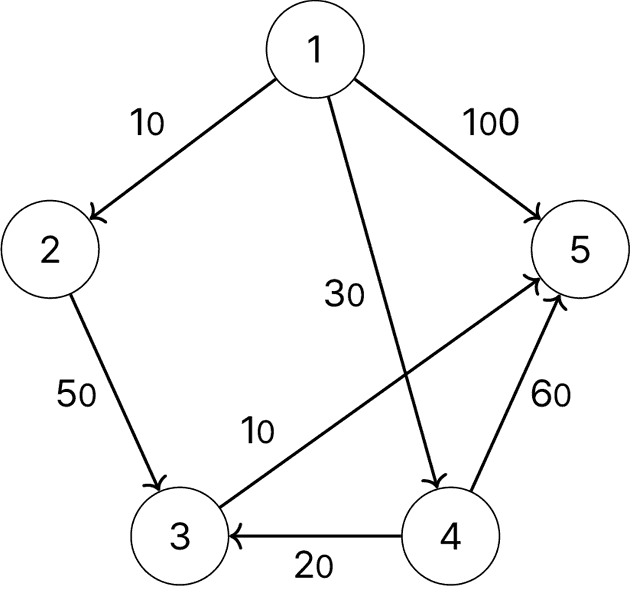
최단 경로 찾기Shortest Path Problem: 다익스트라Dijkstra 알고리즘
e.g.)
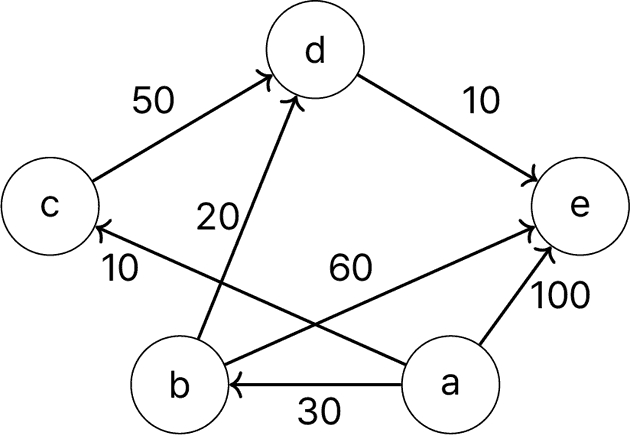
위와 같은 그래프가 주어졌을 때,
D[a] | D[b] | D[c] | D[d] | D[e] | ||
|---|---|---|---|---|---|---|
해밀턴 순회의 응용: 일반적인 해결 알고리즘 존재 X 최근접 이웃 방법Nearest Neighbour Method(Greedy 알고리즘)
그래프의 탐색(Traversal)
-
깊이 우선 탐색Depth First Search; DFS
-
Stack or 재귀로 구현
-
시작 Vertex 에서 인접 Vertex 중 방문하지 않은 Vertex 방문
-
에서 다시 인접 Vertex 중 방문하지 않은 Vertex 방문 반복
-
어떤 Vertex 방문 후 에 인접한 모든 Vertex 방문한 경우, 바로 이전 Vertex로 돌아가 위 반복
-
모든 Vertex 방문 후 탐색 종료
-
-
너비 우선 탐색Breadth First Search; BFS
-
Queue 사용
-
시작 Vertex 에서 인접한 Vertex 모두 차례로 방문
-
더 이상 방문할 Vertex가 없을 때, 다시 에 인접한 Vertex중 처음 방문한 Vertex와 인접한 Vertex 방문
-
에 인접한 Vertex중 두 번째 방문한 Vertex와 인접한 Vertex 방문 반복
-
모든 Vertex 방문 후 탐색 종료
-
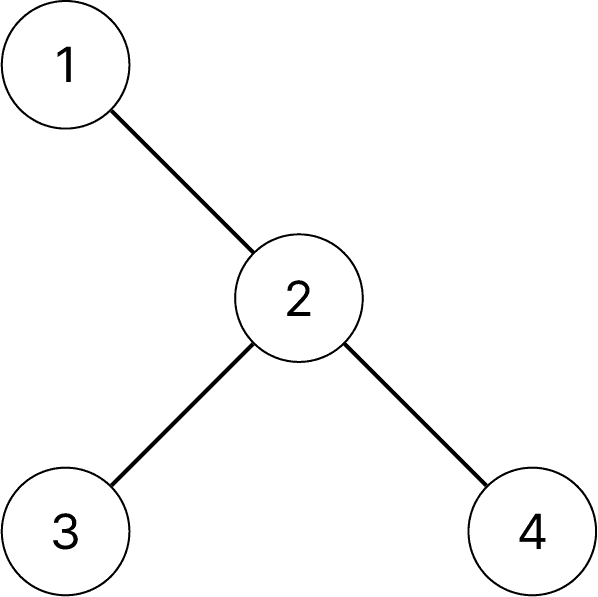
트리Tree
-
A connected undirected graph with no circuits
-
An undirected graph is a tree iff there is a unique simple path between any two of its vertices
-
특별히 지정된 노드인 루트가 있고, 나머지 노드들은 다시 각각 트리이면서 연결되지 않는(disjoint) 은 루트의 서브 트리(Subtree)으로 나누어 진다.
루트Root: 주어진 트리의 시작 노드, 트리의 가장 높은 곳에 위치
차수Degree: 각 노드의 서브 트리의 개수
잎 노드 or 단말 노드Leaf Node: 차수가 0인 노드
자식 노드Children Node: 어떤 노드의 서브 트리의 루트 노드
부모 노드Parent Node: 자식 노드의 반대
형제 노드Sibling Node: 동일한 부모를 가지는 노드
중간 노드Internal Node: 자식 노드를 갖는 노드
조상Ancestor: 루트로부터 각 노드에 이르는 경로 상에 나타난 모든
노드들
자손Descendant: 각 노드부터 잎 노드에 이르는 경로 상에 나타난 모든
노드들
레벨Level: 루트의 레벨 , 자손 노드로 내려가며 ++
트리의 높이 or 깊이Height or Depth: 트리에서 노드가 가질 수 있는
맥스 레벨
숲Forest: 서로 연결되지 않는 트리들의 집합, 트리에서 루트를 제거
숲 생성
는 트리
는 연결되어 있고,
는 연결되어 있고, 어느 한 연결선만을 제거하더라도 는
연결되지 않음
는 사이클을 가지지 않고,
는 어느 한 연결선만 첨가하더라도 사이클 형성
이진 트리
이진 트리Binary Tree: 노드들의 유한 집합, 공집합이거나, 루트와 왼쪽
서브 트리, 오른쪽 서브 트리로 이루어짐
사향 이진 트리Skewed Binary Tree: 왼쪽 or 오른쪽으로 편향된 트리
완전 이진 트리Complete Binary Tree: 높이가 일 때 레벨 부터
까지는 모두 차있고 레벨 에서는 왼쪽 노드부터 차례로 차있는 이진
트리
포화 이진 트리Full Binary Tree: 잎 노드가 아닌 것들은 모두 개씩
자식 노드를 가지며 트리의 높이가 일정할 때
완전 -ary 트리: 레벨이 일 때, 레벨 부터 까지는 모두 n개의
자식 노드를 가지고, 레벨 에서는 왼쪽 노드부터 차례로 차있는 트리
포화 -ary 트리: 모든 중간 노드가 개의 자식 노드를 가지는 트리
포화 -ary 트리에서 개의 중간 노드를 가질 때, 전체 노드 개수
(루트 노드)
이진 트리가 레벨 에서 가질 수 있는 최대 노드 수
높이가 인 이진 트리가 가질 수 있는 최대 전체 노드 수
잎 노드 개수 , 차수가 인 노드 개수 일 때,
항상 성립
이진 트리의 표현
-
배열
-
트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 지울 때 비효율적
-
높이가 인 이진 트리는 각 노드 번호를 인덱스로 하여 1차원 배열로 구현 가능 (인덱스는 1부터 시작)
-
노드 인덱스 의 부모 인덱스
-
노드 인덱스 의 왼쪽 자식 인덱스 , 오른쪽 자식 인덱스
-
-
연결 리스트: 일반적으로 가장 많이 사용. 중간 데이터, 왼쪽 자식 포인터, 오른쪽 자식 포인터 저장
Week 13
이진 트리의 탐방
-
트리의 각 노드를 꼭 한 번씩만 방문Traversal하는 방법
-
각 노드와 그 노드의 서브 트리를 같은 방법으로 탐방
-
전순위, 중순위, 후순위 탐방 기법
-
D: 노드, L: 노드의 왼쪽 서브 트리, R:노드의 오른쪽 서브 트리, 왼쪽을 오른쪽보다 항상 먼저 방문한다고 가정
-
중순위: LDR
-
전순위: DLR
-
후순위: LRD
-
-
수식 표현에서 중순위 표기Infix, 전순위 표기Prefix, 후순위 표기Postfix와 각각 대응
-
탐방의 결과, 각 노드에 들어있는 데이터를 차례로 나열
중순위:
void inOrder(TREE* currentNode) {
if (currentNode != NULL) {
inOrder(currentNode->leftChild);
std::cout << currentNode->data;
inOrder(currentNode->rightChild);
}
}전순위:
void preOrder(TREE* currentNode) {
if (currentNode != NULL) {
std::cout << currentNode->data;
preOrder(currentNode->leftChild);
preOrder(currentNode->rightChild);
}
}후순위:
void postOrder(TREE* currentNode) {
if (currentNode != NULL) {
postOrder(currentNode->leftChild);
postOrder(currentNode->rightChild);
std::cout << currentNode->data;
}
}순회 표기 & 수식 트리
중순위:
전순위:
후순위:
전순위 수식 == 중순위 수식
후순위 수식 == 중순위 수식
-
후순위 표기식과 스택을 활용하여 수식 트리 생성
-
후순위 표기식이 주어지면 스택에 피연산자 저장
-
연산자를 만나면 스택에서 두 개의 피연산자
pop()후 연산 결과(트리) 다시 저장
-
생성 트리와 최소 비용 생성 트리
생성 트리Spanning Tree: 에서 모든 노드들을 포함하는 트리
비용Cost : 트리 연결선의 값의 합
최소 비용 생성 트리(Minimum Spanning Tree: MST): 생성 트리 중 최소 비용
-
Prim's Algorithm
-
에서
-
노드의 집합 를 로 시작
-
일 때, 와 를 연결하는 사이클 형성 X인 가장 짧은 연결선 를 찾아 를 에 포함시킴
-
위를 까지 반복
-
void prim(graph G: set_of_edges T) {
set_of_vertices U;
vertex u, v;
T = NULL;
U = {1};
while (U != V) {
let (u, v) be a lowest cost edge such that u is in U and v is in V - U;
if ((u, v) does not create a cycle) {
T = T |$\cup$| {(u, v)};
U = U |$\cup$| {v};
}
}
}-
Kruskal Algorithm:
-
에서 , (연결선의 집합)
-
Let
-
를 비용이 적은 순서로 정렬
-
가장 최솟값 가진 연결선 차례로 찾아 사이클 형성 X이면 에 포함
-
위를 까지 반복
-
void kruskal(graph G: set_of_edges T) {
T = NULL;
while (T contains less than n - 1 edges and E is not empty) {
choose an edge (v, w) from E of lowest cost;
delete (v, w) from E;
if ((v, w) does not create a cycle in T)
add (v, w) to T;
else discard (v, w);
}
if (T contains fewer than n - 1 edges)
std::cout << "No Spanning Tree";
}트리의 활용
-
문법의 파싱Parsing
-
허프만 코드Huffman Code
-
알파벳 문자를 과 의 비트 코드로 Encoding
-
문자의 발생 빈도에 따라 코드의 길이를 다르게 통신의 효율성
-
접두어 성질: 어떤 문자 코드도 다른 문자 코드의 접두어 코드가 아님
-
-
Huffman Algorithm
-
발생 빈도가 가장 낮은 두 문자를 선택해 하나의 이진 트리로 연결
-
왼쪽 노드에는 빈도수 낮은 문자, 오른쪽 노드에는 빈도수 높은 문자
-
그 두 문자의 루트 노드는 두 문자의 빈도의 합
-
문자들을 이진 트리로 연결
-
그 후에 이진 트리들을 연결
-
-
위 과정을 모든 문자가 하나의 이진 트리로 묶일 때까지 반복
-
생성된 이진 트리의 왼쪽 노드는 , 오른쪽 노드에는 부여
-
루트부터 해당 문자까지 또는 을 순서대로 나열한 것이 해당 문자의 허프만 코드
-
Week 14
이진 탐색 트리Binary Search Tree
-
모든 노드 에 대하여 노드 가 노드 의 왼쪽 서브 트리에 있을 때 이고, 노드 가 노드 의 오른쪽 서브 트리에 있으면 인 이진 트리
-
는 순서 관계를 의미
-
높이 균형 이진 트리인 경우 탐색 시간은
결정 트리Decision Tree
8개의 동전 문제
부울식
0과 1의 조합으로 연산
에 대해 이항 연산자Binary Operator OR과
AND 및 단항 연산자Unary Operator Complement로 표현되는
식
연산 우선 순위:
두 부울식이 같은 진리표Truth Table을 가질 때 동치Equivalent,
연산자는
| 이름 | 법칙 |
|---|---|
| 멱등 법칙Idempotent Law | |
| 항등 법칙Identity Law | |
| 교환 법칙Commutative Law | |
| 결합 법칙Associative Law | |
| 분배 법칙Distributive Law | |
| 흡수 법칙Absorption Law | |
| 역 법칙Inverse Law | |
| 보 법칙Complement Law | |
| 우등 법칙Dominance Law | |
| 드 모르간의 법칙De Morgan's law |
부울 함수Boolean Function
부울 변수와 부울 연산자로 구성된 부울식
개의 부울 변수 에 대한 부울 함수는
으로 표현
개의 부울 변수가 있을 때, 그 변수들로부터 얻을 수 있는 조합은
개
리터럴Literal: 부울 함수를 구성하는 부울 변수 또는 그의 보수
최소항Minterm: 차 부울함수 을 구성하는
논리곱 항들 중 개의 리터럴 곱으로 구성된 항
최소항
부울 함수는 부울 변수에 대한 최소항들 중에서 의 값을 가지는 최소항들의 부울 합을 식으로 표현하는 함수
e.g.)
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
부울 함수는 인 최소항들의 합이므로 이다.
정규식Disjunctive Normal Form; DNF
최소항들의 부울합으로 표현된 부울 함수
최소항들은 부울 변수의 곱으로 표현
곱의 합(Sum of Products) 또는 논리합 표준형
-
정규식이 아닌 부울 함수를 정규식으로 표현하는 방법
-
진리표를 이용한 정규식 변환
-
부울 법칙을 이용한 정규식 변환
-
각 항에 포함되지 않은 부울 변수를 파악
-
각 항에 포함되지 않은 부울 변수에 대해
-
논리곱에 대한 항등 법칙 와
-
논리합에 대한 보수 법칙 을 적용
-
각 항에 없는 부울 변수 추가
-
분배 법칙 등을 이용해 식을 풀고, 중복되는 항은 멱등 법칙에 의해 제거
-
e.g.)
-
예제 풀이
1.
2.
Week 15
부울 함수의 간소화
더 적은 변수와 연산자를 사용하여 같은 기능 또는 결과 도출
-
부울 함수를 간소화 하는 방법:
-
부울식의 기본 법칙 사용 과정이 복잡하고 간소화에 대한 확인이 쉽지 않음
-
카르노맵을 사용
-
-
카르노맵Karnaugh Map
-
부울 함수가 가질 수 있는 모든 경우의 최소항들을 사각형 형태의 표에 배열한 후, 의 값을 가지는 최소항들만 로 표시
- 을 갖는 항들을 연결하여 최소화
-
사각형 내 배치 시, 인접한 최소항들은 변수 하나 차이만 있도록 배치
-
와 은 인접 가능
-
와 은 인접 불가
-
-
-
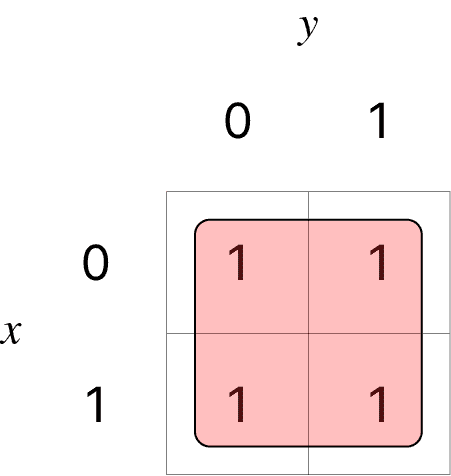
두 변수에 대한 카르노맵: 변수를 라 할 때, 모든 가능한 최소항 조합
-
-
가 이고, 가 일 때, 부울식은
-
(b)
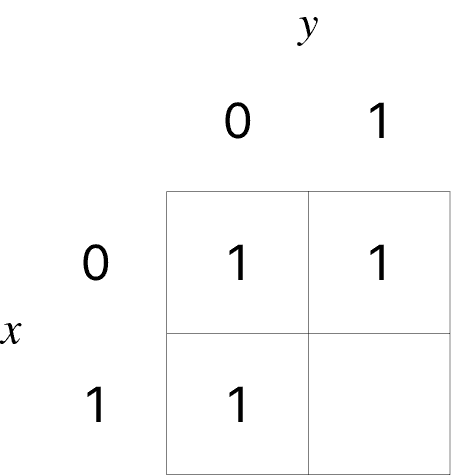
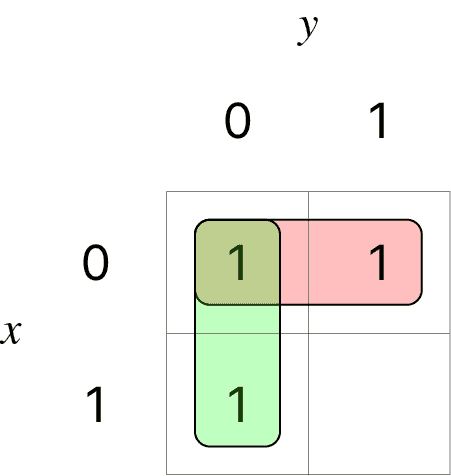
- 간소화: 로 표시된 사각형이 인접할 경우, 함께 묶을 수 있는 경우
e.g.) (a) 인접한 경우 없음:
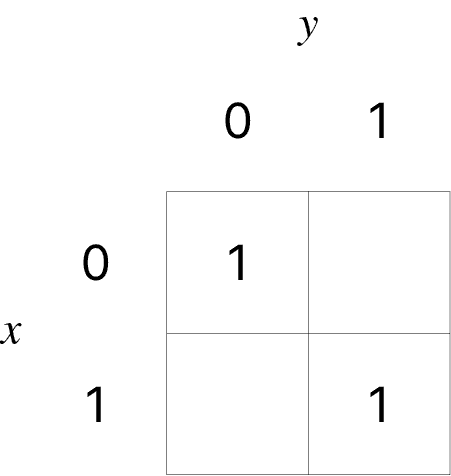 (b) 의 값에 관계없이 의 값이 : (일 때 1)
(b) 의 값에 관계없이 의 값이 : (일 때 1)
 (c) (b)의 경우 + 의 값에 관계 없이
(c) (b)의 경우 + 의 값에 관계 없이
 (d) 와 의 값에 관계없이 항상 1: 1
(d) 와 의 값에 관계없이 항상 1: 1
-
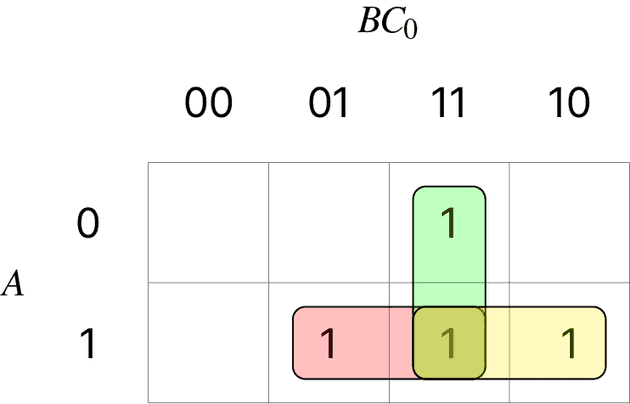
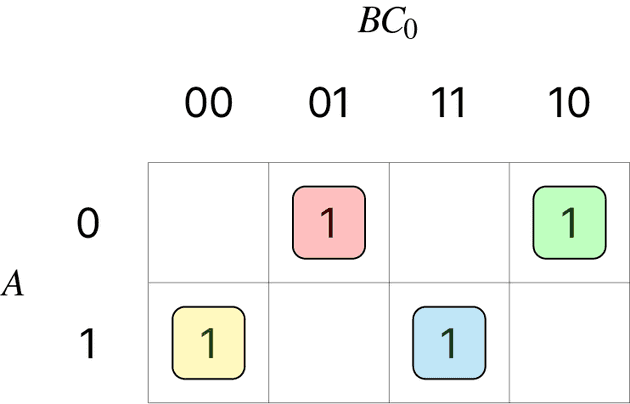
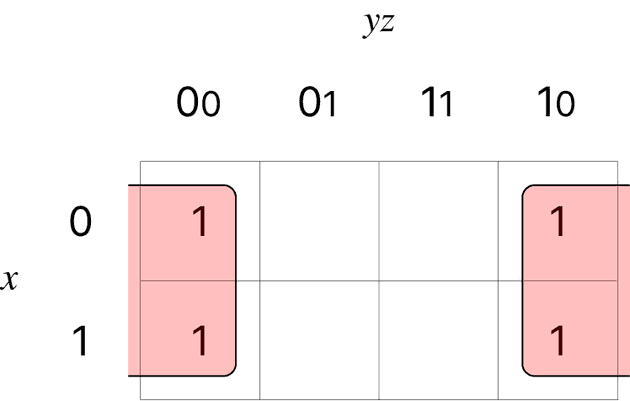
세 변수에 대한 카르노 맵:
-
에 대한 사각형에서 다음에 (인접하는 행 또는 열에서 1비트 차이만 나야함)
-
왼쪽 끝은 오른쪽 끝과 인접하다 생각하기
-
(b)
-
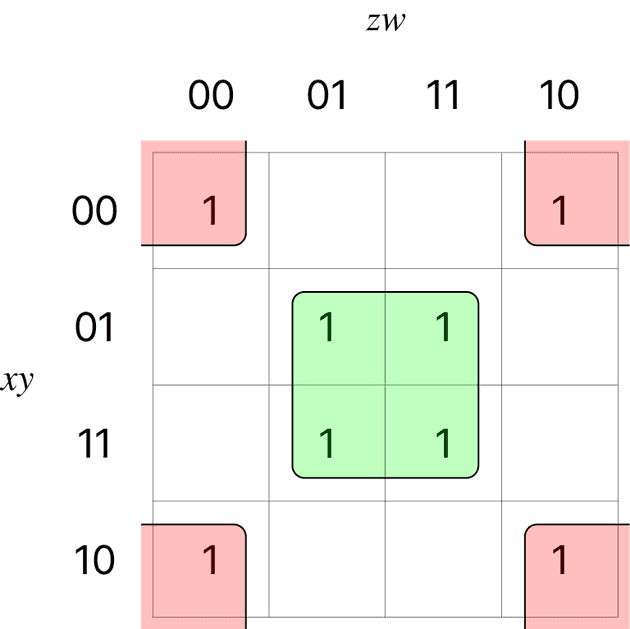
네 변수에 대한 카르노 맵
-
다음
-
왼쪽 끝과 오른쪽 끝 인접
-
위쪽 끝과 아래쪽 끝 인접
-
(b)
논리 회로Logic Circuit
-
논리 회로의 입출력은 논리 게이트Gate들을 상호 연결해 구성
-
입력은 부울 변수, 출력은 부울 함수, 부울 연산자는 게이트
-
= On, = Off
회로를 설계하기 전에 먼저 부울식을 간소화하는 과정이 필요
논리 함수의 완전성Completeness: 부울 연산자 AND, OR, NOT만으로도 모든
논리 함수들을 나타낼 수 있다.
| 게이트 | 기호 | 수식 |
|---|---|---|
| AND |

| |
| OR |

| |
| NOT |
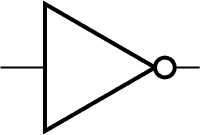
| |
| NAND |

| |
| NOR |

| |
| XOR |

| |
| XNOR |

|
NAND와 NOR의 다른 표현: 드 모르간의 법칙을 적용
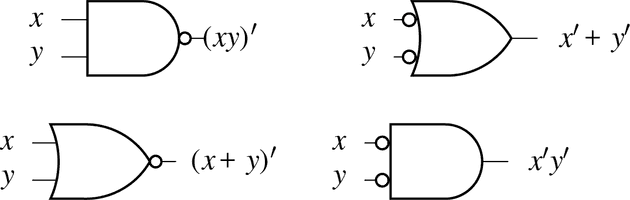
가산기Adder
두 개 이상의 입력을 받아서 이들의 합을 출력
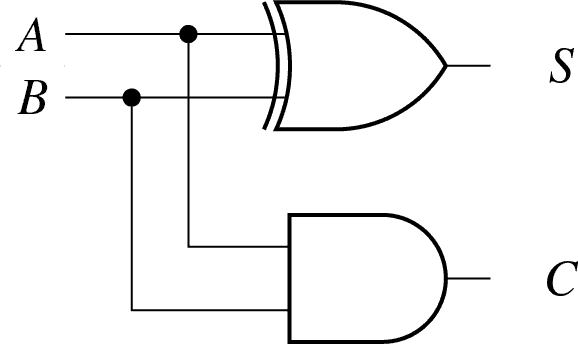
반가산기Half Adder
-
입력: 1비트 정보 두 개
-
출력: 1비트 정보 두 개, 합Sum + 자리 올림Carry
(a) 반가산기의 계산
| 올림수() | 합() | ||
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
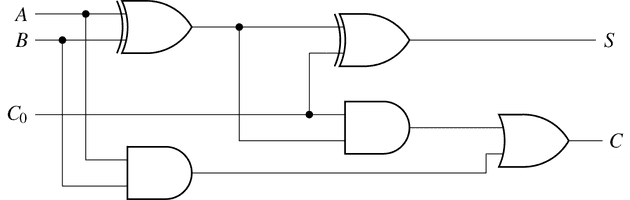
전가산기Full Adder
입력 두 개와 하위 비트에서 발생한 자리 올림수 포함. 2진수 3개 덧셈
전가산기의 계산
| 올림수() | 합() | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
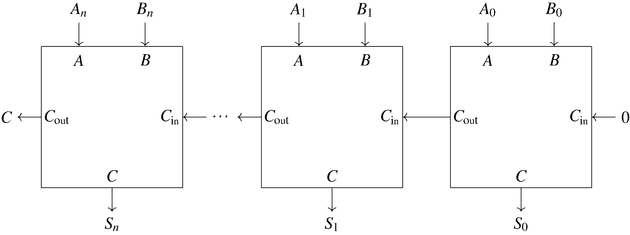
병렬 가산기